Enzymes catalyze reactions, either by virtue of their presence or by specific interactions with the substrate(s). In this course, we will be concerned with two general reaction classes: those that proceed through ES (or ternary) complexes and those that proceed through a substituted enzyme.
For enzymes that form ES (or ternary) complexes (enzyme and substrates are present in the complex)
and follow Michaelis-Menten kinetics, we can develop a general velocity equation as expressed
The latter equation results from ignoring the reversible formation of product.
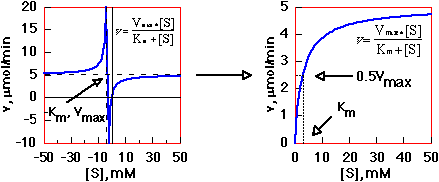
This equation is in the form of a hyperbola, with asymptotes v = Vmax and [S] = -Km. An illustration of this with Vmax = 5 µmol min-1 and [S] = 3 mM appears below. We concern ourselves with only the positive values of [S] and v.
Enzymes that are modified with a transferred group but do not have complete substrates associated with them may be denoted as substituted-enzyme reactions. Visualize the active site and ask if both substrates can fit; you may find that the only way for catalysis to occur is if only a portion of the substrate is transferred to the enzyme before the binding of another substrate. Substituted enzyme kinetics are governed by the rate equations involving multiple substrates. Examples of these reaction mechanisms are a-chymotrypsin, transminases and flavoenzymes.
For example, the pyridoxal-dependent aspartate transaminase reaction may be represented as follows:
Biochemistry and Molecular Biology Home Page
For more information or comments about
this page contact:
eniederhoffer@siumed.edu